|
2024/3/16
|
|
3.14 |
|
|
一昨日3月14日は 「3.14」で円周率の日でした。 小学生の時に 円周や弧の長さ、円の面積を求める際に 毎回、3.14をかけなければならないことに めんどくさいと感じました。 ただ、何回か計算しているうちに、 毎回同じ「3.14」をかけるなら覚えちゃえばいいやと 思うようになり、 1 × 3.14 = 3.14 2 × 3.14 = 6.28 3 × 3.14 = 9.42 4 × 3.14 = 12.56 5 × 3.14 = 15.70 6 × 3.14 = 18.84 7 × 3.14 = 21.98 8 × 3.14 = 25.12 9 × 3.14 = 28.26 を覚えちゃいました。 これでこんな問題は一瞬です。 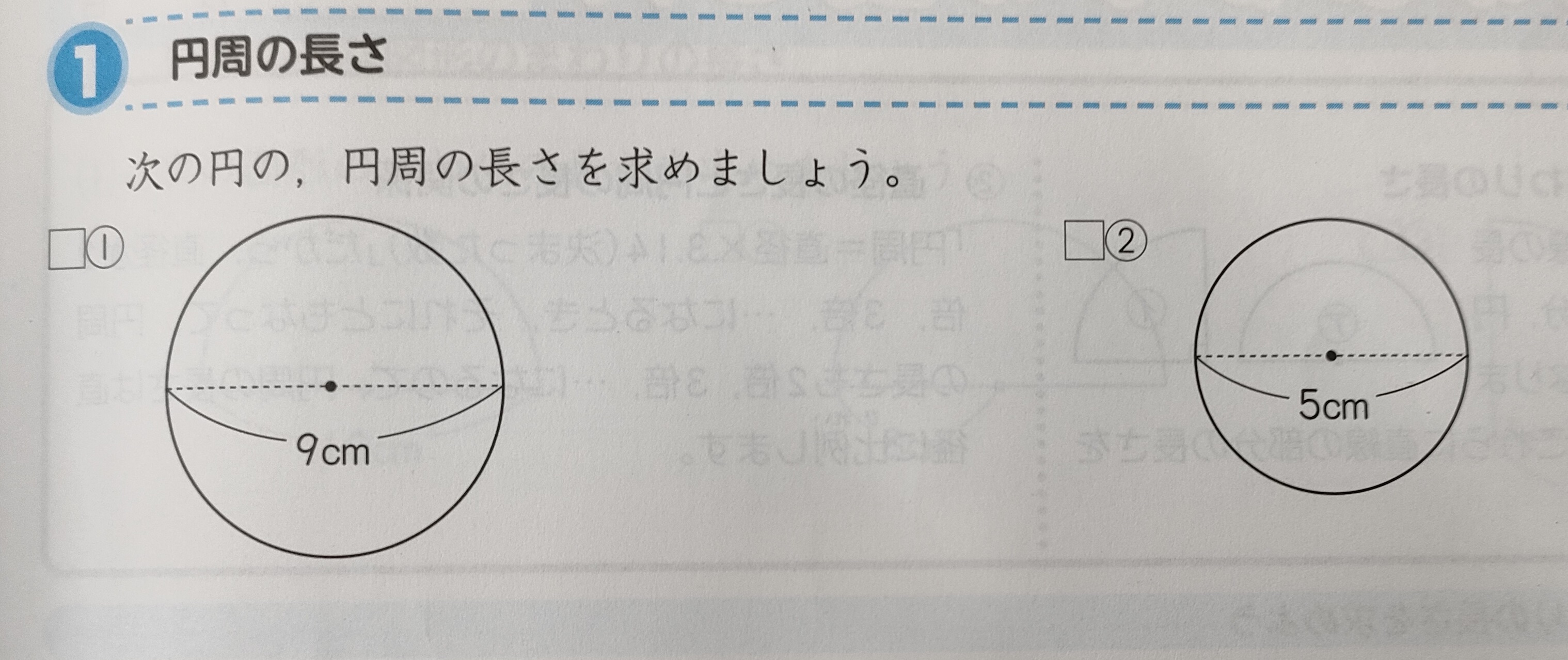 でも、2桁×3.14だとだめじゃない。 いえいえ、そんなことはありません。 一瞬じゃないにしても、 相当速くなります。 58 × 3.14 だって、 3.14 × 58 にしてしまえば、 3.14 × 58 2512←8×3.14の答 1570 ←5×3.14の答 182.12 ほら、足し算をするだけ。 5 × 3.14 を 15.7 ではなく 15.70と覚えたのは 位がずれるのを防ぐため。 これで味をしめた少年時代、 今度は面積用に 4 × 4 × 3.14 = 50.24 5 × 5 × 3.14 = 78.5 6 × 6 × 3.14 = 113.04 7 × 7 × 3.14 = 153.86 8 × 8 × 3.14 = 200.96 9 × 9 × 3.14 = 254.34 も追加で覚えました。 そうしたら、こんな問題なんて 瞬殺!  さらに言えば、 3.14はなるべく最後に計算する。 だって、3.14をかけたら桁数増えて、 そのあとが大変になってしまいますから。 たとえば、 半径6mと半径8mの円の面積の合計なら 6 × 6 × 3.14 + 8 × 8 × 3.14 = 36 × 3.14 + 64 × 3.14 = 113.04 + 200.96 = 314 なんて、全部ひっ算しちゃってたら、 超もったいない。 6 × 6 × 3.14 +8 × 8 × 3.14 = 36 × 3.14 + 64 × 3.14 =(36+64)× 3.14 = 100× 3.14 = 314 みんなが、一生懸命ひっ算している姿を見ながら 暗算で計算できちゃう。 ササっとやって 優越感を感じていました。 今思えば嫌な小学生かもしれませんが、 「何でも要領よく」というのが 当時から私の根底にあった気がします。 |
|
| |
